Avaliação de Modelos de IA com Métricas Tradicionais e Avançadas - Parte 1

Andressa Siqueira
1 de set.
16 min de leitura

1. Introdução

Avaliar modelos de Inteligência Artificial vai muito além de checar se a acurácia é “alta”. Em cenários reais — como saúde, finanças, segurança e recomendação — diferentes métricas respondem a perguntas distintas: o modelo acerta tecnicamente?, gera valor de negócio?, é justo e transparente?

Nestes artigos, vamos falar sobre as três formas de avaliação: métricas diretas (técnicas), métricas indiretas (de impacto/negócio) e métricas éticas (IA responsável). Essa estrutura ajuda a evitar conclusões apressadas (como confiar só na acurácia) e a alinhar o desempenho do modelo aos objetivos e aos riscos do contexto.

Além disso, vamos falar também especificamente de como é calculado cada métrica que conheço e que venho estudando.

2. Tipos de avaliação

2.1. Métricas Diretas (Técnicas)

Também conhecidas como métricas técnicas ou intrínsecas, as métricas diretas são métricas que avaliam diretamente o desempenho do modelo, através da estatística, comparando o seu resultado real com a resultado esperado. Basicamente elas respondem à pergunta: “O modelo funciona bem em prever o que eu pedi para ele prever?”

Uma das suas características é de ser usada no treino, validação e testes, de forma quantitativa, fornecendo uma medida objetiva da precisão e eficácia do modelo. Isso auxilia no ajuste fino do modelo. Alguns exemplos desse tipo de métrica são: Acurácia, Precisão, Recall F1-Score, MSE/RMSE e AUC-ROC.

2.2. Métricas Indiretas

Também são chamadas de extrínsecas, são métricas que não medem diretamente o desempenho técnico do modelo, mas sim o impacto que ele gera nos negócios ou no mundo real refletindo a capacidade da IA de traduzir os dados em valor tangível sendo essenciais para justificar o investimento em IA e demostrar o retorno em relação ao investimento. Basicamente elas respondem à pergunta: "O modelo trouxe valor para o negocio ou para o usuário final?"

2.3. Métricas Éticas (IA Responsável)

Essa métrica avalia se um modelo de IA opera de forma justa, transparente e em conformidade com os valores sociais e regulamentações, incluindo a detecção e mitigação de vieses algorítmicos. Sendo usada para garantir que o modelo não favoreça ou desfavoreça injustamente nenhum grupo. A transparência, a explicabilidade e a auditabilidade também são aspectos importantes da avaliação ética, garantindo que as decisões do modelo possam ser compreendidas e justificadas.

3. Avaliação com Métricas Tradicionais

As métricas tradicionais foram as primeiras a surgirem e formam a base da avaliação dos modelos de IA através do fornecimento de dados quantitativos referentes ao desempenho dos algoritmos.

3.1. Métricas para Modelos de Classificação

Modelos de classificação são algoritmos de aprendizado supervisionados, ou seja, ele aprende, a partir de exemplos rotulados (dados de treino), a atribuir uma classe (categoria) a novas observações.

Alguns algoritmos de classificação são o de Regressão Logística – apesar do nome, é usado para classificação binária, Árvores de Decisão (Decision Trees), Random Forest, SVM, KNN, Redes Neurais Artificiais e o Naive Bayes. Eles são usados para classificar se um email é ou não spam, baseado em um exame se o paciente está saudável ou doente entre outros.

A Matriz de Confusão é a base para a maioria dessas métricas, detalhando os Verdadeiros Positivos (TP), Verdadeiros Negativos (TN), Falsos Positivos (FP) e Falsos Negativos (FN).

3.1.1. Matriz de confusão

A matriz de confusão é uma matriz que resume o desempenho de um modelo de classificação, de forma binária, comparando as predições do modelo com os valores reais (verdadeiros) que mostra a quantidade de acertos e erros do modelo.

A matriz de confusão geralmente compara duas classes (positiva e negativa) e é composta por quatro métricas:

TP (True Positive / Verdadeiro Positivo) → modelo previu positivo e estava certo.
TN (True Negative / Verdadeiro Negativo) → modelo previu negativo e estava certo.
FP (False Positive / Falso Positivo) → modelo previu positivo, mas era negativo (chamado de erro tipo I).
FN (False Negative / Falso Negativo) → modelo previu negativo, mas era positivo (chamado de erro tipo II).

Essas quatro siglas representam as quatro formas em que os nossos modelos podem acertar e errar. T vem de True, ou verdadeiro. F vem de False, ou falso. P vem de Positive, positivo. E N de Negative, negativo. As quatro letras formam essas quatro combinações. [1]

Um dos principais motivos para ser a base de avaliações dos modelos de classificação é que a matriz de confusão mostra não apenas o número de acertos, mas onde o modelo está errando o que permite identificar viés de classe (quando o modelo acerta mais uma classe do que outra).

3.1.2. Métricas Básicas (Tradicionais)

Acurácia (Accuracy)

Ela mede a proporção de previsões corretas em relação ao total de previsões, calculada como (TP + TN) / (TP + TN + FP + FN). Usando um exemplo simples, se o seu modelo faz 100 previsões e acerta 85 delas, sua acurácia é de 85%.

Mas a acuraria alta nem sempre é boa, principalmente em quando você tem dados desequilibrados ou desbalanceados, ou seja, você tem mais dados de uma classe do que de outra. Uma das formas de mitigar esse erro, é usar duas ou mais métricas na hora de avaliar o seu algoritmo.

Um ótimo exemplo disso é dado por [1] e vou trazer para você. Não vou tentar criar um exemplo se já tem um ótimo! Para fins didáticos e de exemplificação, vamos supor que nós estamos construindo um modelo para prever se um tumor é maligno (classe Positiva 1) ou benigno (classe Negativa 0). Suponhamos que nossa base de treino tenha 100 exemplos, onde 91 são benignos (classe Negativa 0) e 9 tumores são malignos (classe Positiva 1).

Treinamos o nosso modelo sobre os 100 exemplos e na hora de avaliá-lo temos a seguinte Matriz de Confusão.

Matriz de Confusão: Classificação de tumores. [1]

Temos uma Acurácia de 91%, pois acertamos 91 predições de um total de 100 exemplos. Parece muito bom o nosso modelo, certo? Errado.

Vamos olhar um pouco mais de perto os erros do nosso modelo.

Dos 91 tumores benignos, o modelo conseguiu prever corretamente 90 como benignos e isso é bom. Entretanto, dos 9 tumores malignos, o modelo conseguiu identificar apenas 1! Um resultado terrível. 8 das 9 pessoas com tumores malignos não foram diagnosticadas corretamente pelo modelo."

Precisão (Precision)

Diferente da acurácia que vê todos as previsões certas, aqui o foco é na qualidade calculada como (TP / (TP + FP)). Ela pode ser resumida na pergunta: “De todas as previsões que o modelo classificou como Positivo, quantas ele acertou?”.

Utilizando ainda o exemplo dado por [1], se extrairmos os valores de Verdadeiros Positivos (TP) e de Falsos Positivos (FP) para aplicar a formula teremos (1/(1+1)) = 0,5, ou seja, o modelo quando ele prevê que um tumor é maligno (classe Positiva 1), ele está correto 50% das vezes. Já notamos uma diferença bem grande dos 91% de acurácia, não é?

Mas atenção, um modelo pode ter alta precisão e ainda assim ser ruim, se ele “jogar seguro” e só classificar como fraude casos muito óbvios, deixando passar várias fraudes (o que afetaria o Recall).

Recall

Também chamado de Revocação, Taxa de Cobertura, Taxa de Captura, e Sensibilidade, dependendo do autor, mostra a proporção de casos positivos reais que o modelo conseguiu identificar, calculada como (TP/(TP+FN)). Ele responde a seguinte pergunta: “De todos os positivos existentes, quantos eu consegui encontrar?”

Ainda utilizando o exemplo dado por [1], sim, utilizaremos bastante ele, e aplicando a formula teremos (1 /(1+8)) = 0,11, ou seja, o modelo só identifica corretamente 11% dos tumores malignos. Se pensarmos nas áreas da saúde e segurança, esse numero é baixíssimo!

Dica: Se o seu recall der 1.0, ou seja 100%, significa que não houve nenhum falso negativo.

Mas atenção, normalmente, o Recall e a precisão são inversamente proporcionais, ou seja, aumentarmos a Precisão nós diminuímos o Recall e vice-versa. O que vai definir qual métrica terá maior peso na sua análise é o seu objetivo, do momento da sua empresa e área de aplicabilidade do seu algoritmo.

F1-Score

Também conhecido como F-score e F-measure, é a média harmônica entre a precisão e o recall, logo, ele leva em consideração tanto os erros de Falso Positivos (FP) quanto os de Falso Negativos (FN) sendo calculado através da formula: ((2*Precisão*Recall)/(Precisão+Recall))

Dica: Usamos o F1-Score quando os valores de precisão e recall são importantes.

Essa medida utiliza a média harmônica porque ela dá mais importância a valores baixos isso significa que aumentar o valor da F1-Score é aumentar simultaneamente a Precisão e a Recall

Utilizando os valores de Recall e Precisão encontrados antes, temos o seguinte calculo para o F1-Score: ((2*0,5*0,11)//(0,11+0,5))= 0,18. Considerando o problema proposto por [1], temos um valor baixíssimo, o que nos mostra que seria necessário rever todo nosso algoritmo para tentarmos melhorar o F1-Score.

Especificidade (Specificity)

Ela mede a capacidade do modelo de identificar verdadeiros negativos. É a proporção de negativos verdadeiros em relação aos negativos reais, TN / (FP + TN). Em outras palavras: “De todos os exemplos que realmente eram negativos, quantos o modelo classificou corretamente como negativos?”

A diferença entre a especificidade e a Recall é que uma foca nos negativos reais (saudáveis, transações legítimas, não fraude) enquanto o outro foca nos positivos reais (doentes, fraudes, anomalias).

Atenção, um modelo com alto Recall, mas baixa especificidade pode sobrecarregar o sistema com falsos positivos

Vamos analisar o exemplo dado por [1]:

Para o calculo de especificidade temos (90/(90+1)) = 0,989, ou seja, esse modelo tem altíssima especificidade, ou seja, ele é muito bom em reconhecer os negativos reais (no caso, classificar corretamente exemplos da classe 0).

Por outro lado, olhando para os positivos reais (Recall), vemos que o modelo teve baixo desempenho, já que identificou apenas 1 dos 9 positivos (sensibilidade ≈ 11,1%). Esse comportamento é comum em datasets desbalanceados, quando o modelo “aprende” a priorizar a classe majoritária (neste caso, os negativos).

AUC-ROC

A curva ROC (Receiver Operating Characteristic) representa a relação entre o Recall e a Especificidade, em diferentes limiares de decisão. O valor do AUC mede a área sob essa curva e indica a capacidade do modelo em separar as classes:

AUC = 1,0 significa um modelo perfeito;
AUC = 0,5 significa um modelo equivalente a escolhas aleatórias;
Valores abaixo de 0,5 indicam desempenho pior que o acaso.

Quando plotamos esse ponto na curva ROC para as métricas de Recall e Especificidade calculadas do exemplo dado por [1] , percebemos que a área sob a curva (AUC) fica em torno de 0,55. Isso é bem próximo de 0,5, ou seja, quase como se o modelo estivesse chutando.

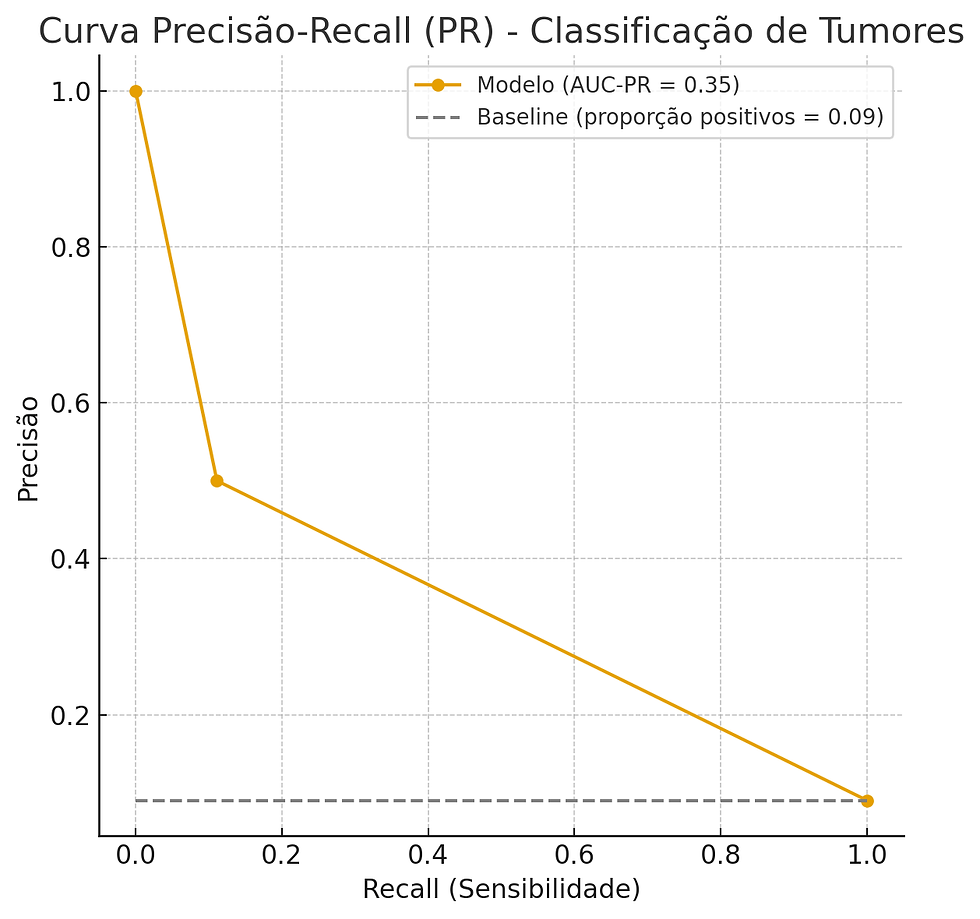
AUC-PR

A curva PR mostra a relação entre Precisão e Recall sendo especialmente útil em bases desbalanceadas, porque foca diretamente na classe positiva.

O valor AUC-PR varia de 0 a 1, quanto mais a curva se afasta do baseline em direção ao canto superior direito (alta precisão e alto recall), melhor é o modelo.

1,0 = modelo perfeito (sempre acerta todos os positivos sem gerar falsos positivos).
próximo do baseline = modelo ruim, quase como adivinhar.
abaixo do baseline = pior que o acaso.

Analisando em cima do exemplo dado por [1] temos que a precisão é de 0,50 e o Recall é de 0,11. Ao gerar toda a curva PR:

AUC-PR ≈ 0,35
A linha de base (baseline) é a proporção de positivos na base de dados: 9/100 = 0,09.

Isso mostra que o modelo tem desempenho acima do acaso, já que o AUC-PR (0,35) é maior que o baseline (0,09), mas ainda é muito fraco: acerta apenas metade das vezes quando diz que um tumor é maligno, e encontra pouquíssimos casos positivos (Recall baixo). Em termos práticos, o modelo não é confiável para diagnóstico: perde 8 em cada 9 casos de tumor maligno.

3.1.3. Métricas Avançadas

MCC

O Matthews correlation coefficient é uma métrica de classificação que leva em conta todos os valores da matrix de confusão. Por isso, é uma métrica que muitos consideram como mais confiável, já que atinge altos valores apenas quando as previsões obtém bons resultados mesmo quando as classes estão desbalanceadas.

Ela é calculada através da formula abaixo e tem seu valor variando entre -1 e 1.

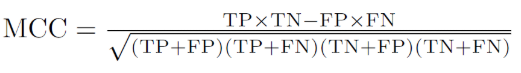
Seu resultado pode ser avaliado da seguinte forma:

+1 → classificação perfeita.
0 → desempenho equivalente ao acaso.
-1 → classificação totalmente incorreta (predições inversas).

Aplicando essa métrica ao exemplo dado por [1] temos que o MCC é igual a 0,205 que está bem próximo de 0, o que indica que o modelo tem pouco poder de correlação entre previsões e realidade. Apesar da acurácia alta (91%), o MCC mostra que o modelo não é realmente bom, pois ignora a maioria dos positivos (tumores malignos).

Kappa de Cohen

Ele é uma estatística que mede o nível de concordância entre duas classificações categóricas (neste caso, entre as previsões do modelo e os valores reais).

Diferente da acurácia, que só olha para a proporção de acertos, o Kappa leva em conta que parte desses acertos poderia ocorrer por puro acaso.

Ela é calculada atraves da formula: k= ((Po -Pe)/(1-Pe) onde,

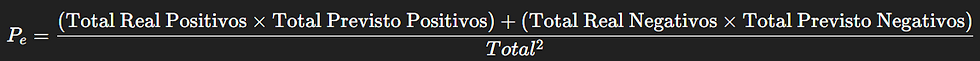
Sendo interpretada como:

κ = 1 → concordância perfeita.
κ = 0 → concordância equivalente ao acaso.
κ < 0 → concordância pior que o acaso.

Usando o exemplo dado por [1] temos o seguinte cenário:

Total Real Positivos = 9
Total Real Negativos = 91
Total Previsto Positivos = TP + FP = 2
Total Previsto Negativos = TN + FN = 98

Po = (1+90)/100 = 0,91

Pe = ((9*2)+(91*98))/(100*100)= 0,8936

k=(0,91-0,8936)/(1-08936) = 0,154.

Esse resultado indica apenas concordância leve entre as previsões do modelo e os valores reais. Isso confirma que, apesar da acurácia de 91%, o modelo não é bom para identificar tumores malignos. O Kappa revela que o desempenho está muito próximo de um classificador aleatório que sempre chutaria “benigno”.

Log Loss

Também chamado de Logarithmic Loss ou Cross-Entropy Loss, mede a performance de um classificador probabilístico. Diferente da acurácia, que só olha se o modelo acertou ou errou penalizando mais fortemente previsões erradas feitas com alta confiança.

Calculado através da equação

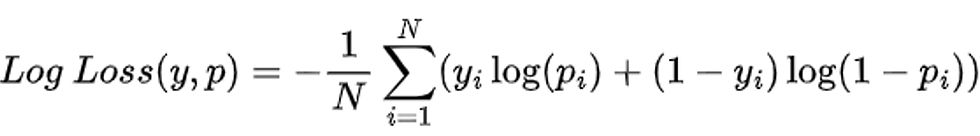
Onde:

N = número de amostras.
yi = valor real (0 ou 1).
pi = probabilidade prevista da classe positiva.

Seu resultado varia de:

0 → modelo perfeito.
∞ → modelo muito ruim.

Atenção: a matriz de confusão dada por [1] não traz probabilidades, apenas decisões finais (0 ou 1). Para calcular o Log Loss corretamente, precisaríamos das probabilidades de cada previsão. Então, para fins didáticos, vamos assumir que o modelo atribuiu probabilidade 1,0 às classes que previu, ou seja:

Para casos classificados como positivos → previu 100% de chance de ser positivo.
Para casos classificados como negativos → previu 100% de chance de ser negativo.

Para os acertos (TP=1, TN=90):−log⁡(1)=0-\log(1) = 0−log(1)=0 (sem penalidade) e para os erros (FP=1, FN=8): Como o modelo errou com 100% de confiança, temos:−log⁡(0)-\log(0)−log(0) → que tende ao infinito. Ou seja, o modelo não está bem calibrado.

3.2 Métricas para Modelos de Regressão

MAE

O Erro Médio Absoluto (em inglês, Mean Absolute Error) calcula média dos erros entre os valores previstos e os valores reais através da soma das diferenças absolutas entre as previsões e as observações, dividida pelo número de amostras.

Quando fazemos contas de diferença (real – previsto), os erros podem ser positivos (quando chutamos para menos) ou negativos (quando chutamos para mais). Se somarmos direto, alguns erros se cancelariam, e pareceria que o modelo não errou tanto. Por isso usamos o valor absoluto (o tamanho do erro, sem sinal). Assim, todo erro conta como erro.

Vamos nos basear no seguinte exemplo: Imagine que você está tentando prever o preço de casas:

Casa 1 → Preço real: 500 mil | Preço previsto: 480 mil | Erro: 20 mil
Casa 2 → Preço real: 600 mil | Preço previsto: 590 mil | Erro: 10 mil
Casa 3 → Preço real: 700 mil | Preço previsto: 720 mil | Erro: 20 mil
Casa 4 → Preço real: 800 mil | Preço previsto: 750 mil | Erro: 50 mil

Isso nós dá o MAE igual à (20+10+20+50)/4=25

Isso significa que o modelo erra, em média, 25 mil reais ao prever os preços das casas. Ou seja, quando pego um valor previsto, sei que ele pode estar, em média 25 mil reais mais caro ou mais barato.

MSE

O Erro Quadrático Médio mede o erro médio entre os valores reais e os valores previstos, elevando cada erro ao quadrado antes de calcular a média. Isso significa que erros pequenos contam pouco e que erros grandes contam muito mais, porque são ampliados ao quadrado. É uma métrica que penaliza fortemente erros grandes.

Usando o exemplo das casas, temos

Casa 1 → Preço real: 500 mil | Preço previsto: 480 mil | Erro: 20 mil| Erro ao quadrado: 400 mil
Casa 2 → Preço real: 600 mil | Preço previsto: 590 mil | Erro: 10 mil| Erro ao quadrado: 100 mil
Casa 3 → Preço real: 700 mil | Preço previsto: 720 mil | Erro: 20 mil| Erro ao quadrado: 400 mil
Casa 4 → Preço real: 800 mil | Preço previsto: 750 mil | Erro: 50 mil| Erro ao quadrado: 2500 mil

Isso nós dá o MSE igual à (400+100+400+2500) /4 = 850

O MSE está em unidades ao quadrado (milhões de reais, neste caso), o que dificulta um pouco a interpretação direta.

RMSE

Também chamado de raiz do erro quadrático médio, ele mede o tamanho médio dos erros do modelo, mas com um detalhe importante: Primeiro, eleva os erros ao quadrado (como no MSE), o que dá mais peso aos erros grandes. Depois, tira a raiz quadrada, para trazer o valor de volta à mesma unidade da variável prevista.

Assim, o RMSE mostra, em média, o quanto o modelo erra em relação ao valor real, mas sendo mais sensível a grandes diferenças. Para calcular basta tirar a raiz quadrada do MSE.

Dica: Quanto menor o RMSE, melhor o modelo.

Usando o exemplo das casas, temos a raiz quadrada de 850 é aproximadamente 29,15. Isso significa que, em média, o modelo erra 29 mil reais nas previsões de preço das casas.

MAPE

Que é o erro percentual médio absoluto, mostra, em média, quanto o modelo erra em termos percentuais em relação ao valor real. Diferente do MAE ou RMSE, que medem o erro em valores absolutos, o MAPE traz o erro em %. Isso torna a métrica fácil de interpretar e comparar em diferentes contextos.

Ele é calculado como a soma das diferenças percentuais absolutas entre as previsões e as observações, dividida pelo número de amostras.

Usando o exemplo de casas, temos:

Casa 1 → Preço real: 500 mil | Preço previsto: 480 mil | Erro: 20 mil| Erro %: 4%
Casa 2 → Preço real: 600 mil | Preço previsto: 590 mil | Erro: 10 mil| Erro %: 1,67%
Casa 3 → Preço real: 700 mil | Preço previsto: 720 mil | Erro: 20 mil| Erro %: 2,86%
Casa 4 → Preço real: 800 mil | Preço previsto: 750 mil | Erro: 50 mil| Erro %: 6,25%

Fazendo o MAPE temos: (4+1,67+2,86+6,25)/4 = 3,7%. Isso significa que, em média, o modelo errou 3,7% nos preços das casas.

Também chamado de Coeficiente de Determinação, mede quanto da variação dos dados reais é explicada pelo modelo, ou seja, mostra o quanto bem o modelo consegue representar os dados reais. Ele é calculado através da equação 1 -(SSE/SST), onde:

SSE (Sum of Squared Errors) = soma dos erros ao quadrado do modelo.
SST (Total Sum of Squares) = soma dos erros ao quadrado usando a média dos valores reais como previsão.

Vamos usar o exemplo das casa para ficar mais fácil

Casa 1 → Preço real: 500 mil | Preço previsto: 480 mil | Erro: 20 mil
Casa 2 → Preço real: 600 mil | Preço previsto: 590 mil | Erro: 10 mil
Casa 3 → Preço real: 700 mil | Preço previsto: 720 mil | Erro: 20 mil
Casa 4 → Preço real: 800 mil | Preço previsto: 750 mil | Erro: 50 mil

Primeiro calculamos a média dos valores reais: (500+600+700+800)/4 =650

Depois calculamos a variação total (SST) = (500−650)^2+(600−650)^2+(700−650)^2+(800−650)^2 = 50.000

Então calculamos o erro do modelo (SSE)= (500−480)^2+(600−590)^2+(700−720)^2+(800−750)^2= 3.400

Agora podemos calcular o R² = 1 -(3400/50000) = 0,932

Isso significa que 93% da variação dos preços das casas é explicada pelo modelo. Ou seja, o modelo é bem ajustado: ele captura grande parte da relação entre as variáveis (ex.: tamanho, localização, número de quartos) e o preço das casas, apesar de não garantir que o modelo fará boas previsões em novos dados.

MedAE

O erro absoluto mediano é muito parecida com o MAE. A diferença é que, em vez de calcular a média dos erros absolutos, ele calcula a mediana. Isso torna ele menos influenciável a outliers.

Vamos usar o exemplo das casa

Casa 1 → Preço real: 500 mil | Preço previsto: 480 mil | Erro: 20 mil
Casa 2 → Preço real: 600 mil | Preço previsto: 590 mil | Erro: 10 mil
Casa 3 → Preço real: 700 mil | Preço previsto: 720 mil | Erro: 20 mil
Casa 4 → Preço real: 800 mil | Preço previsto: 750 mil | Erro: 50 mil

Pegando os erros e os colocando em ordem, temos: [10, 20, 20, 50]. A mediana é a média dos dois valores centrais (20 e 20), ou seja, nesse caso, o MedAE é igual a 20. Isso significa que, em uma previsão típica, o modelo erra cerca de 20 mil reais no preço da casa.

Comparação e Discussão

Os dois exemplos apresentados, o diagnóstico de tumores para algoritmos de classificação e a previsão de preços de casas para algoritmos de regressão, mostram como métricas diferentes podem contar histórias distintas sobre um mesmo modelo.

No caso dos tumores, a Acurácia sozinha parecia satisfatória, mas outras métricas revelaram as falhas graves. Recall mostrou que o modelo deixou de identificar a maioria dos tumores malignos. Enquanto a Precisão e F1-Score expuseram a baixa qualidade geral das previsões positivas. AUC-ROC e AUC-PR mostraram que o poder de separação entre classes é quase aleatório e o MCC e Kappa confirmaram baixa concordância e pouca correlação entre predições e realidade.

Esse conjunto evidencia que, em cenários críticos e desbalanceados, confiar apenas na acurácia pode levar a conclusões perigosas.

No caso dos preços das casas, as métricas de regressão mostraram como métricas de regressão se complementam: algumas trazem clareza prática (MAE, MAPE), enquanto outras expõem a influência dos erros extremos (MSE, RMSE) ou o grau de ajuste global (R²).

No conjunto, os dois cenários reforçam a lição central: não há métrica única que responda a todas as perguntas. Cada métrica destaca um aspecto do modelo e só a análise combinada permite uma avaliação confiável.

Conclusão

Avaliar modelos de IA exige olhar além da primeira impressão. Métricas diferentes revelam limitações e potenciais que, isoladamente, passariam despercebidos. Mais do que escolher uma métrica, é fundamental combiná-las de acordo com o objetivo do negócio e o risco do domínio.

Na Parte 2, vamos explorar outras métricas avançadas e práticas de avaliação, ampliando essa visão para que tenhamos um kit de ferramentas completo na hora de analisar os modelos.

Então me conta, você conhecia todas essas métricas?

Referências

[1] LOPES, A. Medidas de Performance: Modelos de Classificação -. Disponível em: <https://brains.dev/2023/medidas-de-performance-modelos-de-classificacao>. Acesso em: 24 ago. 2025.

‌ [2]FILHO, M. O Que É Acurácia Em Machine Learning? Disponível em: <https://mariofilho.com/o-que-e-acuracia-em-machine-learning>. Acesso em: 24 ago. 2025.

[3] Medium. Disponível em: <https://medium.com/@mateuspdua/machine-learning-m>. Acesso em: 24 ago. 2025.

[4] FILHO, M. Precisão, Recall e F1 Score Em Machine Learning. Disponível em: <https://mariofilho.com/precisao-recall-e-f1-score-em-machine-learning>. Acesso em: 1 set. 2025.

‌[5]KUNDU, R. F1 Score in Machine Learning: Intro & Calculation. Disponível em: <https://www.v7labs.com/blog/f1-score-guide>.

[6] PEDIGO, M. Sensibilidade e especificidade: Um guia completo. Disponível em: <https://www.datacamp.com/pt/tutorial/sensitivity-specificity-complete-guide>. Acesso em: 1 set. 2025.

[7] PETRO SAMOSHKIN. Explore the nuances of evaluating machine learning model performance through widely used metrics like the F1 Score and the Matthews Correlation Coefficient (MCC). This article delves into real-world examples, technical explanations, and the advantages of MCC, providing valuable insights for AI engineers. Learn how to optimize model predictions in scenarios ranging from customer relationship improvement to logistics network optimization. Disponível em: <https://www-linkedin-com.translate.goog/pulse/f1-score-matthews-correlation-coefficient-mcc-petro-samoshkin-xscwf?_x_tr_sl=en&_x_tr_tl=pt&_x_tr_hl=pt&_x_tr_pto=tc>. Acesso em: 1 set. 2025.

‌[8] IBM. Matriz de confusão. Disponível em: <https://www.ibm.com/br-pt/think/topics/confusion-matrix>.

‌[9] CHICCO, D.; JURMAN, G. The Matthews correlation coefficient (MCC) should replace the ROC AUC as the standard metric for assessing binary classification. BioData Mining, v. 16, n. 1, 17 fev. 2023.

[10] Classification: ROC and AUC. Disponível em: <https://developers-google-com.translate.goog/machine-learning/crash-course/classification/roc-and-auc?_x_tr_sl=en&_x_tr_tl=pt&_x_tr_hl=pt&_x_tr_pto=tc>.

[11] Viera, A. J., & Garrett, J. M. (2005). Understanding interobserver agreement: The kappa statistic. Family Medicine, 37(5), 360–363.

[12] GUPTA, A. Learn how to evaluate the quality and goodness of fit of machine learning models for regression problems using three more metrics: MPE, MAPE, and R-Squared. This article will explain what each metric means, how to calculate it, and how to interpret it. Disponível em: <https://www-linkedin-com.translate.goog/pulse/understanding-machine-learning-model-evaluation-metrics-ayush-gupta-yejle?_x_tr_sl=en&_x_tr_tl=pt&_x_tr_hl=pt&_x_tr_pto=tc>. Acesso em: 1 set. 2025.

‌[13] GEEKSFORGEEKS. How to Calculate Mean Absolute Error in Python? Disponível em: <https://www-geeksforgeeks-org.translate.goog/python/how-to-calculate-mean-absolute-error-in-python/?_x_tr_sl=en&_x_tr_tl=pt&_x_tr_hl=pt&_x_tr_pto=tc>. Acesso em: 1 set. 2025.

‌[14] WAPLES, J. Erro absoluto médio explicado: Medindo a precisão do modelo. Disponível em: <https://www.datacamp.com/pt/tutorial/mean-absolute-error>. Acesso em: 1 set. 2025.

‌[15] Glossary: Data Science - Mean Absolute Error | C3 AI. Disponível em: <https://c3-ai.translate.goog/glossary/data-science/mean-absolute-error/?_x_tr_sl=en&_x_tr_tl=pt&_x_tr_hl=pt&_x_tr_pto=wa>. Acesso em: 1 set. 2025.

‌[16] Medium. Disponível em: <https://medium.com/@ia.bb/interpreta>. Acesso em: 1 set. 2025.

[17] Discover thousands of collaborative articles on 2500+ skills. Disponível em: <https://www.linkedin.com/pulse/m>.

‌